Арифметика

О Русской Классической Школе на телеканале «Союз». Выпуск 5
О наглядности при изучении математики, об особенностях учебных пособий А. С. Пчёлко и Г. Б. Поляка, а также о том, что не бывает абсолютных гуманитариев и все дети могут быть способными к математике, рассказывает разработчик математического блока Русской Классической Школы, тренер-методист Е. М. Нифонтова.

О Русской Классической Школе на телеканале «Союз». Выпуски 14 и 15
О реформах в сфере образования в XX и XXI веках и об их последствиях, о принципах классического обучения детей и о том, с помощью чего можно вернуться к ним, рассказывает И. П. Костенко, разработчик математического блока Русской Классической Школы, кандидат физико-математических наук, доцент.

История методики обучения математике в начальной школе
Лекция по истории методики обучения математике, прочитанная Т. А. Алтушкиной, руководителем проекта РКШ, на семинаре в 2017 году. Это очень объёмный и насыщенный материал, который позволит вам получить детализированное представление о том, как складывалась судьба начального математического образования в нашей стране с момента его зарождения вплоть до наших дней.

Ретроспективный анализ реформирования математического образования в России
Доклад И. П. Костенко, кандидата физико-математических наук и разработчика математического блока в образовательной системе «Русская Классическая Школа», представленный им на Рождественских чтениях в 2016 году.

Опыт работы по классической методике математики в современной школе
Доклад Е. М. Нифонтовой, разработчика математического блока в образовательной системе «Русская Классическая Школа», представленный ею на Рождественских чтениях в 2016 году.

Обучающий семинар по арифметике в начальной школе. Симферополь, 2017 г.
В чём особенность классической методики обучения детей математике? Чем отличаются современные способы подачи учебного материала от классических? Из-за чего математика часто кажется детям трудной? Как сделать так, чтобы ребёнок глубоко понимал всё, чему мы его учим? Как же учить детей, чтобы они любили математику и не боялись её? Поиск ответов на эти вопросы — в следующем видео.

Обучающий семинар по арифметике в начальной школе. Екатеринбург, 2017 г.
В этом семинаре, как и в его предыдущей версии, рассказывается о классической методике обучения детей математике. Он представлен более красиво и структурно; также некоторые темы в нём даны подробнее, например, нумерация и обучение решению задач. Это последний семинар, который проводили сами разработчики Русской Классической Школы (Т. А. Алтушкина и Е. М. Нифонтова).

Т. А. Алтушкина — Советы начинающим преподавать арифметику по классической методике
Прежде чем браться за обучение детей по классическим учебникам, нужно понять основные отличия классической методики от современных принципов обучения, которые игнорируют наглядно-образную и предметно-деятельную природу детского восприятия.

Т. А. Алтушкина — Из методики обучения решению задач

Т. А. Алтушкина — Феи математики как симулякры мотивации
Как нам вбили в головы, что неотъемлемый элемент современного урока — мотивационная часть! Что прежде чем приступать к работе, нужно обязательно искусственно простимулировать познавательную мотивацию, пригласить незнаек, гномиков, фей (продолжите сами) и сделать акцент на «осознанности» усвоения знаний...

В. П. Урлапова — Об ошибках в применении методик РКШ
Чем больше педагогов и родителей использует методики Русской Классической Школы, тем больше мы видим искажений и ошибок в их применении. Некоторые из них мы рассмотрим в данной статье. Очень надеемся, что она поможет нашим читателям избежать подобных ошибок в обучении детей по нашей программе.

Изучение нумерации многозначных чисел в начальной школе
В начальной школе дети постепенно знакомятся с числами от простых единиц до сотен миллиардов, узнают разряды и классы многозначных чисел; на этой основе учатся правильно читать и записывать большие числа.

Всероссийские проверочные работы по математике и годовые контрольные РКШ по арифметике
Предлагаем вашему вниманию подробное сравнение между ВПР по математике и годовыми контрольными работами РКШ по арифметике для 4 класса.

В. П. Урлапова — О наглядности в математике
Мы с вами знаем, что в начальной школе у детей доминирует наглядно-образное мышление. Поэтому хорошая методика обязательно должна использовать этот ресурс, чтобы ребёнок мог опираться на него в изучении и понимании материала. Разберёмся в том, как это делается в классической методике и современных образовательных программах, и сделаем выводы, как эффективно использовать наглядно-образное мышление для обучения детей математике.
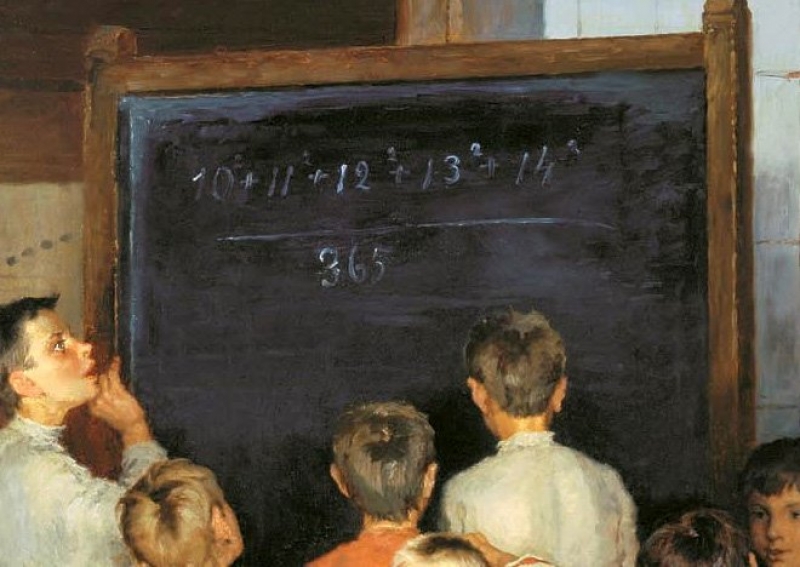
В. П. Урлапова — О пользе устного счёта
В программе математических дисциплин Русской Классической Школы особое место принадлежит устному счёту. Как спортсмены начинают тренировку с разминки, так и детям полезно каждый урок арифметики или алгебры начинать со счёта в уме. Устный счёт — это великолепная тренировка ума! Давайте разберёмся, какие функции нашего ума развиваются при систематическом устном счёте.

В. П. Урлапова — Что делать, если ребёнку не даётся устный счёт?
Предложив ребёнку решить устно тот или иной интересный с нашей точки зрения пример, мы можем столкнуться с тем, что ему, в отличие от нас, совсем не так интересно его решать, что в счёте он делает систематические ошибки, нервничает, не хочет считать и так далее. Предлагаем разобраться, в чём причины подобных затруднений и как их преодолеть.

В. П. Урлапова — Что такое математическая тревожность и как с ней бороться?
Одно исследование показало, что математическая тревожность практически не коррелирует с общей тревожностью. Значит, есть ученики, эмоционально стабильные и уверенные в себе, которыми овладевает паника, стоит им только столкнуться с математической задачей. Очевидно, причина математической тревожности не в «тревожном» складе личности, а в чём-то другом! В чём же?

В. П. Урлапова — О схемах, кратких записях и смысле жизни
Краткая запись для решения задачи, а не задачи для кратких записей! В этом заключается природосообразность — краткая запись начинает использоваться именно тогда, когда ребёнок сам замечает в ней смысл.
В. П. Урлапова — Об алгоритмах, нестандартных задачах и математическом интеллекте
Эта статья написана в ответ на стремление некоторых родителей или педагогов, впервые столкнувшихся с программой по арифметике Русской Классической Школы, чем-то её дополнить, разбавить или даже взять лишь часть курса, «только основное», а другую часть — из других программ.

Е. В. Барышева — Научиться видеть задачу глазами ребёнка
Данная статья посвящена анализу ошибок, допущенных при решении текстовых задач.

Е. В. Барышева — Рисунок или формальная схема: что поможет в обучении?
Здесь рассказывается об иллюстрировании задач: что представляют из себя такие иллюстрации, когда их вводить, как правильно использовать.
