При просматривании классических учебников Пчёлко и Поляка по арифметике, их внешней простоты и системности многим людям, привыкшим к пестроте и фрагментарности современных учебников математики, не хватает в них нестандартных, так называемых логических задач. Мы не раз слышали это обвинение… Попробуем ответить на него.
В классической методике обучения арифметике самое ценное — система постепенно усложняющихся типовых задач, где их сложность нарастает постепенно, но неуклонно: сначала однотипные постепенно усложняющиеся задачи, затем новый тип изученных задач даётся вперемешку с ранее изученными типами, чтобы у ребёнка не возникало шаблонности мышления. Такая система даёт возможность ученикам в 6 классе решать ОЧЕНЬ сложные задачи, но при этом чувствовать себя уверенными в своих силах (так как они пришли сюда очень постепенно, как по лесенке взошли). Пример такой задачи в 17 действий приводит Е. М. Нифонтова в конце своего доклада.
Если же ребёнка обучать математике только на логических задачах, которые не систематизированы, то это бесперспективно. Объясним почему: в логической задаче всегда присутствует фактор полной неожиданности, ребёнок к ней не подготовлен предыдущей системной работой, он каждый раз чувствует себя неуверенно, в каждой задаче — подвох. Это рождает ощущение беспомощности.
Однако это не означает, что от таких задач нужно совсем отказаться. В нашем курсе таких нетиповых, так называемых занимательных задачек много в третьем и четвёртом классах. Они находятся не в учебнике, а в поурочных планах на устном счёте. Мы использовали два замечательных пособия, которые размещены у нас на сайте в разделе «Библиотека», — «Занимательные задачи» Г. Б. Поляка и «Внеклассная работа по арифметике в начальной школе» В. А. Игнатьева.
Из них мы выбирали те задачки, которые, как нам казалось, наиболее интересны и в то же время посильны для детей. Эти пособия использовались учителями в советское время для внеклассной работы, для математических кружков. Очень рекомендуем всем!


Повторим, что в наших поурочных планах много занимательных задач из этих пособий. Приведём несколько примеров ниже.
***
3 класс
Урок № 150. Занимательная задача «Бой часов»:
Настя сидела за уроками 3 часа и каждый раз прислушивалась к бою стенных часов, считая количество ударов. Часы били каждый час, и Настя насчитала всего 18 ударов. С какого часа по какой она сидела за уроками?
Урок № 155. Занимательная задача «Лакомки»:
Мама купила конфеты и положила их в шкаф. Тима пришёл из школы, увидел в шкафу конфеты и съел половину их. Кира пришла второй из школы и, найдя конфеты в шкафу, съела половину остатка. Давид пришёл из школы третьим и съел половину конфет, которые остались после Киры. Когда мама взяла вечером пакет с конфетами, то в нём оказалась всего 1 конфета. Сколько конфет купила мама?
Урок № 166. Занимательная задача «Сколько лет дедушке?»:
Внук спросил дедушку: «Сколько тебе лет?» Дедушка ответил: «Если проживу ещё половину того, что я прожил, да ещё 1 год, то мне будет 100 лет». Сколько лет дедушке?
4 класс
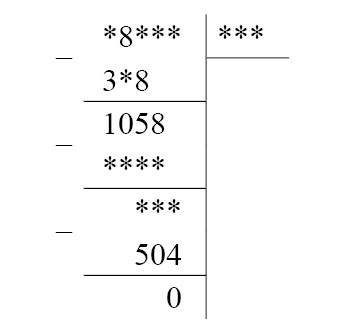
Урок № 184. Найдите, какие цифры стёрты:
Урок № 187. Занимательная задача:
Настенные часы забегают вперёд на 20 секунд в час. В полдень 1 января 2012 года их стрелки установили верно. Через какое время часы снова покажут правильное время?
Урок № 193. Угадывание чисел:
— Задумайте число, которое делится без остатка на 6. Сложите теперь половину этого числа с одной третьей и одной шестой частями. Что у вас получилось?
— У вас получилось задуманное число. Почему это так?
***
При этом после каждой задачи учителю даётся подсказка, как лучше направить ребёнка к решению в случае затруднения таким образом, чтобы не решить за него, а только натолкнуть мысль на верный путь, — смотрите ниже.
***
3 класс
Урок № 150. Занимательная задача «Бой часов»:
Настя сидела за уроками 3 часа и каждый раз прислушивалась к бою стенных часов, считая количество ударов. Часы били каждый час, и Настя насчитала всего 18 ударов. С какого часа по какой она сидела за уроками?
— Кто из вас слышал бой часов? Как можно, не глядя на часы, а только слушая их, узнать, который час?
Рассуждение при решении задачи: часы били 3 раза по несколько ударов. Очевидно, что во второй раз они ударили на 1 удар больше, чем в первый; а в третий раз на 2 удара больше, чем в первый. Если не принимать во внимание 3 эти удара, то в остальном часы били каждый раз одинаковое количество ударов (с этого момента большинство детей смогут решить задачу):
1) 18 уд. – 3 уд. = 15 уд.
2) 15 уд. : 3 уд. = 5 уд. — пробили часы в первый раз.
— Значит, Настя сидела за уроками с пяти до восьми часов. Когда она села, часы пробили 5 ударов, через час — 6 ударов, ещё через час — 7 ударов; а к тому времени, как часы собирались пробить 8 ударов, она уже сделала все уроки.
Урок № 155. Занимательная задача «Лакомки»:
Мама купила конфеты и положила их в шкаф. Тима пришёл из школы, увидел в шкафу конфеты и съел половину их. Кира пришла второй из школы и, найдя конфеты в шкафу, съела половину остатка. Давид пришёл из школы третьим и съел половину конфет, которые остались после Киры. Когда мама взяла вечером пакет с конфетами, то в нём оказалась всего 1 конфета. Сколько конфет купила мама?
Задача решается с конца: 1 оставшаяся конфета — это половина того, что съел Давид. Значит, он съел 1 конфету, а всего в шкафу, когда он пришёл, лежало 2 конфеты. Две конфеты — это половинка того, что съела Кира. Значит, когда она пришла к шкафу, там лежало 4 конфеты. Четыре конфеты — это половинка того, что съел Тима, значит, изначально в пакете было 8 конфет.
Урок № 166. Занимательная задача «Сколько лет дедушке?»:
Внук спросил дедушку: «Сколько тебе лет?» Дедушка ответил: «Если проживу ещё половину того, что я прожил, да ещё 1 год, то мне будет 100 лет». Сколько лет дедушке?
В случае затруднения предложить детям следующую схему:
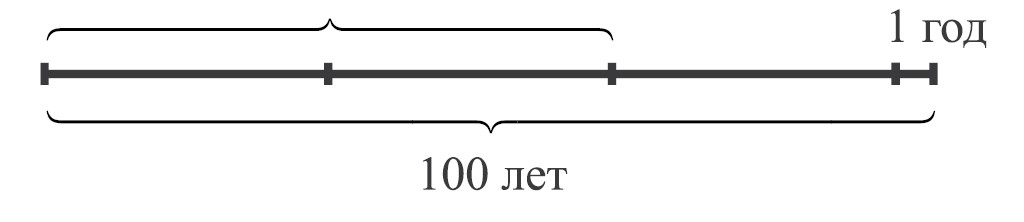
— Дедушка прожил вот столько (учитель чертит первый отрезок), если он проживёт ещё половину этого (делит его пополам и добавляет отрезок, равный половине первого) да ещё 1 год (добавляет маленький отрезок), то дедушке будет 100 лет.
4 класс
Урок № 184. Найдите, какие цифры стёрты:

В случае затруднения учитель помогает наводящими вопросами:
— В примере не известны ни делимое целиком, ни делитель, ни частное. Можем ли мы подобрать хоть одну цифру вместо звёздочек в этих числах? (Нет.) А посмотрите на остаток в примере. Чему он равен? (Нулю.) От какого-то числа вычли 504 и получили 0. Чему равно это число? (504.) Впишите эти цифры:
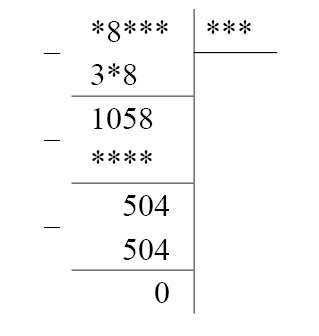
— Из числа 1 058 вычли какое-то число и получили 50, да ещё списали 4. Можем найти это число? Найдите и впишите цифры:
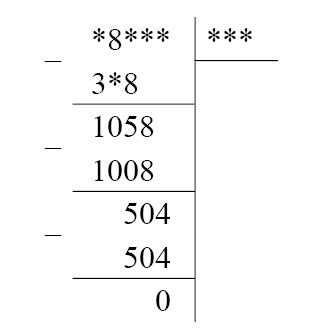
— Можем ли мы теперь найти последние 2 цифры делимого? (Можем, это 8 и 4):

— Попытаемся восстановить оставшиеся цифры делимого и числа, которое из него вычитается. От какого числа нужно отнять 8, чтобы осталось 5? (От 13) Какую цифру впишем над 8? (3):

И так далее…
Урок № 187. Занимательная задача:
Настенные часы забегают вперёд на 20 секунд в час. В полдень 1 января 2012 года их стрелки установили верно. Через какое время часы снова покажут правильное время?
В случае затруднения учитель помогает наводящими вопросами:
— Посмотрите на циферблат наших часов (они должны быть с секундной стрелкой) и скажите, на сколько уйдут часы вперёд через 3 часа, если за час они убегают на 20 секунд? (На 1 минуту.) Значит, можно сказать так: погрешность часов за 3 часа составит 1 минуту. За какое время накопится погрешность в 3 минуты? (За 9 часов, так как 3 час. × 3 = 9 час.) За какое время убегут часы на 1 час вперёд? (За 180 часов, так как 3 час. × 60 = 180 час.)
— Часы будут всё убегать и убегать. Посмотрите на часы и подумайте, какой должна стать погрешность часов, на сколько они должны забежать вперёд, чтобы показания стрелок снова совпали с реальным временем? (На 12 часов.) Значит, для того чтобы узнать, когда же часы снова покажут правильное время, нужно высчитать, за какой промежуток времени накопится погрешность в 12 часов. (180 часов × 12 = 2 160 часов.)
Дети производят вычисления, переводят часы в сутки (2 160 часов : 24 часа = 90 суток), затем задача решается, как обычная задача на вычисление времени окончания события. Важным моментом в задаче является то, что 2012 год был годом високосным, то есть в феврале было 29 дней. Следовательно, если отсчитать 90 суток от полудня 1 января, то искомое событие приходится на полдень 1 апреля.
Урок № 193. Угадывание чисел:
— Задумайте число, которое делится без остатка на 6. Сложите теперь половину этого числа с одной третьей и одной шестой частями. Что у вас получилось?
— У вас получилось задуманное число. Почему это так?
От сложения половины с третьей и шестой частью единицы всегда получается единица. Поэтому когда мы складываем вместе половину задуманного числа, третью и шестую часть его, мы получаем в сумме задуманное число.
***
Итак, наше преимущество в том, что у нас есть и система (!), и иногда фактор неожиданности, который не пугает ребёнка, а повышает интерес.
Обратите внимание на то, что мы не даём нестандартные задачи в первых двух классах — ждём, пока дети обретут первые вычислительные навыки, войдут в системную логику курса. В 3 и 4 классах мы не даём нестандартные задачи одновременно с новой темой, так как это отвлечёт силы ребёнка от главного. Занимательные задачи всегда появляются на уроках закрепления изученного материала, когда основная часть урока понятна и легка. Они освежают и бодрят ум.
