Мы с вами знаем, что в начальной школе у детей доминирует ещё наглядно-образное мышление. Поэтому хорошая методика обязательно должна использовать этот ресурс, чтобы ребёнок мог опираться на него в изучении и понимании материала.
Разберёмся в том, как это делается в классической методике и современных образовательных программах, и сделаем выводы, как эффективно использовать наглядно-образное мышление для обучения детей математике.
Современные фгосовские учебники пестрят яркими картинками. Ёжики, домики, мишки, зайки, яркие, разноцветные, утрированно искажённые изображения с нарушенными пропорциями, как будто нарисованные неумелой детской рукой, — и это всё, чтобы сделать такую книжку ближе и роднее её основному читателю — ребёнку… Казалось бы, это хорошо и правильно, ведь не что иное, как картинка, запускает процесс наглядно-образного мышления. Всё верно. Но зададим себе вопрос — куда, в каком направлении эта картинка запускает данный процесс? В сторону понимания и усвоения учебного материала или в ином направлении? Привлекает внимание к теме урока или отвлекает от неё? Помогает ребёнку сконцентрировать внимание или рассеивает его? Одна мама призналась мне как-то, что, когда она смотрит на разноцветную мультяшную пестроту учебников и рабочих тетрадей, у неё болит голова. Задумаемся: что тогда происходит с ребёнком, если даже взрослый, гораздо лучше владеющий собой, начинает испытывать дискомфорт?..

Классические учебники, напротив, выполнены в сдержанной, деловой манере. Весь их стиль говорит ребёнку о том, что учёба — это труд, а не развлечение, и относиться к нему следует серьёзно. В учебнике арифметики цветные картинки встречаются только в самом начале, иллюстрации используются только для понимания материала и только там, где это необходимо.
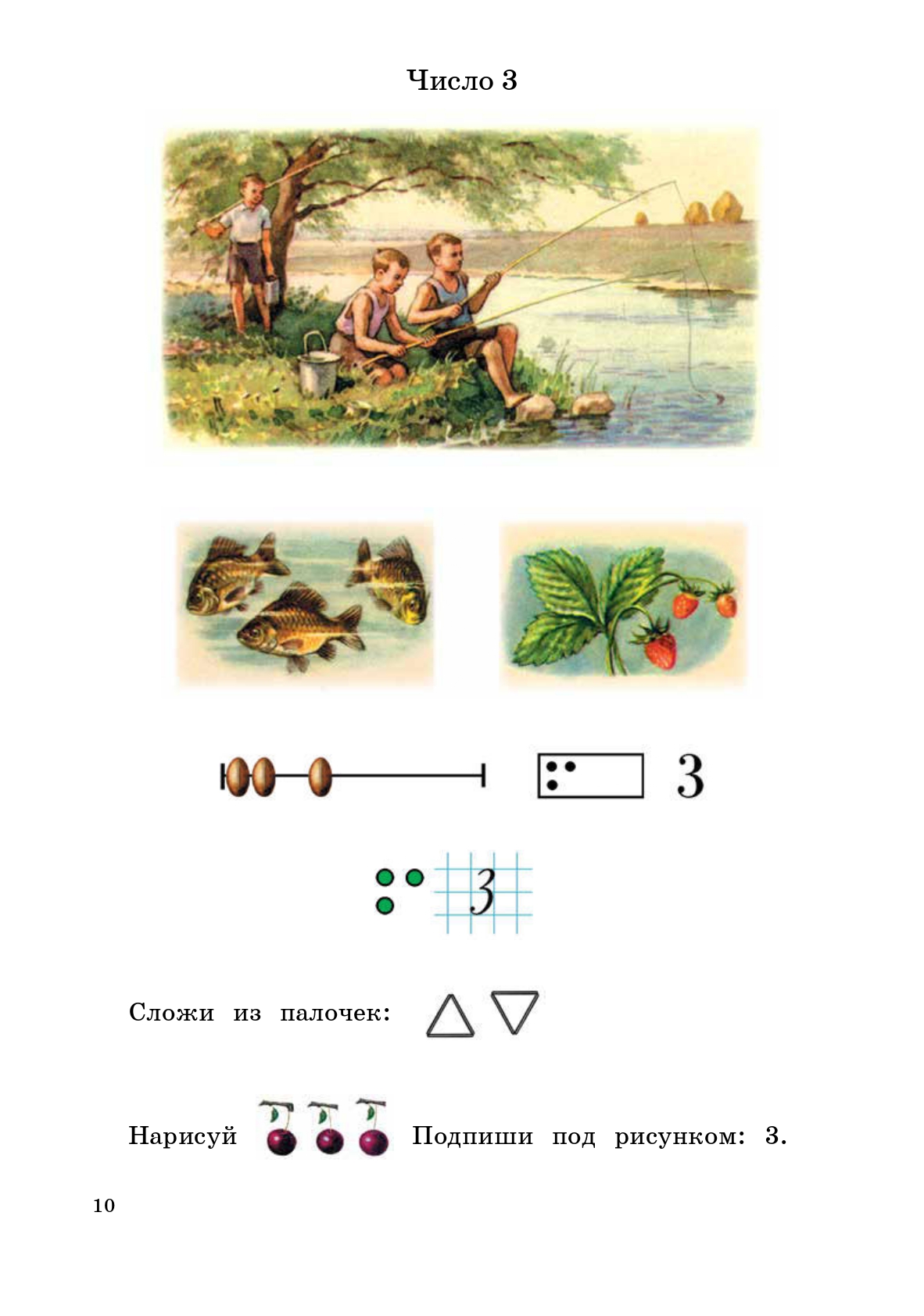

«А как же опора на наглядно-образное мышление?», — спросите вы. В Русской Классической Школе её достаточно! При решении примеров активно используется счётный материал. Дети имеют чёткое наглядное представление, что такое десяток, сотня, тысяча — отдельные палочки связываются в десятки, десятки — в сотни.

При изучении объёма используются кубики размером в 1 см³, которыми измеряются параллелепипеды разного размера, а позже, в стереометрии, — объёмные модели геометрических тел, благодаря чему у старшеклассников при слове «октаэдр» или «додекаэдр» в голове возникает не туман, а вполне конкретное образное представление.

А какой восторг испытывают первоклашки, когда они кладут один кубик на брусок из 10 кубиков — дцать — и получают «один-на-дцать»… «три-на-дцать»… «восемь-на-дцать»! Мой сын не меньше недели с горящими глазами рассказывал об этом всем вокруг. И это понятно — перед ним приоткрылась не только глубина математики или языка, но и тайна мудрого мироустройства вообще!
Получить более полное представление об использовании наглядности в математике вы можете, посмотрев наши ролики на Youtube. Обратим также ваше внимание на то, что в классической методике используется не только наглядно-образное мышление, но и наглядно-действенное, ведь дети не только смотрят на картинки, но и активно действуют с дидактическим материалом! Собственными руками прибавляют и отнимают нужное количество палочек, развязывают и связывают десятки, практически, а не по теоретической схеме осуществляя переход через разряд. И где больше наглядности? Где крепче связь знаний с чувственным опытом — в классической методике или в современных разноцветных учебниках и рабочих тетрадях?
Отдельно хочется сказать об использовании схем для решения текстовых задач.
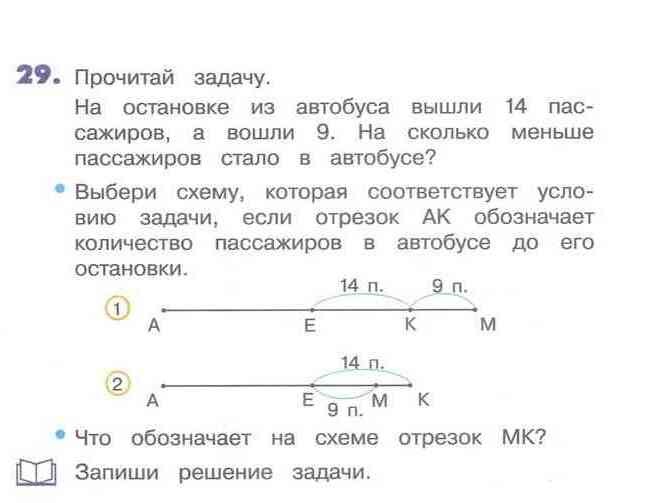
В современных методиках активно используются схемы-отрезки.
«На поляне летали 3 бабочки, и ещё 2 бабочки сидели на цветках. Сколько всего бабочек было на лугу?»
Для решения подобных задач используются схемы-отрезки. И это начинается даже не в первом классе, а в детском саду. Что это? Использование наглядно-образного мышления? На первый взгляд — да. Рисунок же. Но по существу это — попытка с детского сада внедрить теоретико-множественный подход к решению простейших арифметических задач. Слова «множество» и «подмножество» для детей трудны и очень между собой похожи, путать будут. Поэтому заменим их словами «целое» и «часть». А любое множество будем условно представлять в виде отрезка. Тогда часть отрезка будет изображать подмножество данного множества. И вот эта абстракция загружается в голову ребёнка с помощью схем-отрезков. Зачем?
В одной из наших статей мы уже обращали ваше внимание на то, что в классической природосообразной методике краткая запись задачи используется только тогда, когда её необходимость очевидна ребёнку, если он сам чувствует, что без неё трудно удержать в голове задачу. То есть — когда она помогает ребёнку. То же самое относится к чертежам, схемам, рисункам.
Помогают ли детям схемы-отрезки решить задачку про бабочек? Очевидно, не только не помогают, но и мешают. А какой наглядный материал помог бы ему решить задачу? Ну, конечно же, рисунок. 3 бабочки слева и 2 бабочки справа. Или счётный материал.
Учитель: «Положи перед собой столько красных кружков, сколько бабочек летает. Сколько их, давай посчитаем!»
Ученик: «Три».
Учитель: «А теперь положи рядом с ними столько жёлтых кружков, сколько бабочек сидит на цветках! Сколько их, посчитай!»
Ученик: «Два!»
Учитель: «Сколько всего кружков?»
Ученик: «Пять!»
Учитель: «Сколько всего бабочек?»
Ученик: «Пять!»
Всегда ли это нужно? Конечно, нет! Если есть трудность с решением задачи, используем этот метод. Если ребёнок легко решил и без наглядного материала — он не нужен! Это будет тормозить его мышление.
Вернёмся к схемам-отрезкам. Мы уже поняли, что их использование не природосообразно. Для полноты картины хотелось бы добавить, что оно ещё и математически и логически некорректно! Поэтому многократное его повторение из урока в урок искажает математическое и логическое мышление ребёнка.
Нельзя трёх бабочек представить в виде отрезка, потому что три бабочки — это множество, состоящее из 3 элементов, а отрезок — это континуум, бесконечное множество! Теория множеств — достаточно сложный раздел математики, и не все сразу осознают тот факт, что на отрезке в один сантиметр точек больше, чем целых чисел на всей числовой прямой. Человек же, с детства привыкший изображать трёх бабочек в виде отрезка, не поймёт этого никогда! Парадокс: с детского сада внедряем теорию множеств, чтобы к окончанию школы ребёнок пришёл полностью неспособным к её пониманию.
Вторая некорректность — логическая. Она касается использования понятия целого. Целое — это не арифметическая сумма частей, а нечто большее. Пять бабочек на поляне или три тарелки на столе — это не целое! Целое подразумевает некоторое внутреннее единство (целостность), т. е. взаимосвязь между частями. Молекула (целое) состоит из атомов (частей), связанных химическими связями, организм (целое) состоит из взаимосвязанных между собой органов (частей), машина (целое) собирается из деталей (частей) по определённой схеме, текст (целое) строится из предложений (частей), выстроенных в соответствии с логикой повествования и т. д. В случае с тремя бабочками или семью цветочками такой связи нет, поэтому и употреблять понятие «целое» здесь некорректно.
Вы можете возразить: ребёнок этого пока не понимает, поэтому ничего страшного, если мы сложное понятие «множество» заменим более простым — «целое». На данном этапе сойдёт и так, вырастет — разберётся. Нет! Не сойдёт! При обучении детей математике (как, впрочем, и другим наукам) употребление понятий должно быть точным и правильным! Тогда и у ребёнка будет формироваться последовательное и ясное логическое мышление.
Неграмотное употребление понятий грубо искажает детскую логику, закладывает бомбу замедленного действия в развитие мышления. Тем более, если это ключевое понятие, многократно повторяемое на каждом уроке.
Есть множество вариантов отношений между понятиями. С раннего детства осваивая родной язык, ребёнок интуитивно постигает это разнообразие логических связей. Постепенно он начинает чувствовать, что, к примеру, связь «птица — крыло» не такая же, как связь «пять монеток — одна монетка», и не такая же, как «ягода — малина».

Недопустимо под видом наглядности или другого дидактического приёма вносить искажения и хаос в формирующуюся логическую структуру мышления ребёнка! Схемы-отрезки и использование отношения «часть-целое» для решения простых задач на сложение грибочков и цветочков — это совершенно ненужная и вредная «наглядность»!
Когда же уместны и нужны схемы-отрезки? Например, при решении задач на движение. Расстояние между пунктом А и пунктом В совершенно правильно будет изобразить отрезком. Также вполне правомерно разделить его на две части, обозначающие расстояния, пройденные каждым пешеходом (автомобилем, поездом и т. п.) до места их встречи. Их пути в сумме будут составлять — нет, ни в коем случае не целое! — общее расстояние между населёнными пунктами.
Теперь допустим, что нам предстоит решить такую задачу:
«Поле площадью 852 га засеяли овощами. При этом свёклы посеяли в 2 раза больше, чем моркови, а огурцов – в 6 раз больше, чем свёклы. Сколько гектаров засеяно каждым из овощей?»
Полезна здесь будет наглядная схема? Вполне возможно! Как будем изображать площади и их соотношения? Помогут ли нам схемы-отрезки? Гораздо удобней и понятней для ребёнка будет, если мы изобразим площади квадратиками. Наименьшую часть, засеянную морковью, представим в виде одного квадратика. Тогда часть, засеянная свёклой, будет составлять 2 таких квадратика, а огурцами — 12. С таким наглядным представлением задача решается легко и удобно.
Подведём итоги сказанному выше:
1. Учитывая преобладание у младшего школьника наглядно-образного мышления, классическая природосообразная методика обучения математике использует наглядные способы представления изучаемого материала: счётный материал, рисунки, схемы для лучшего понимания структуры задачи и смысла выполняемых действий.
2. Иллюстрации должны содержать то, и только то, что нужно для понимания материала. Ничего лишнего, рассеивающего и отвлекающего!
3. Наглядное представление материала должно облегчать, а не усложнять и не затуманивать его понимание. Рисунок или схема – не самоцель, а средство решения задачи.
4. Способы наглядного и графического представления материала должны быть строго адекватны тому, что они изображают. Если задача о предметах — используем рисунки предметов или счётный материал, если о расстояниях — отрезки, о площадях — плоские фигуры (например, квадраты), об объёмах — объёмные тела (например, кубики).
Следуя этим простым принципам, педагог может эффективно использовать наглядно-образное мышление ребёнка для обучения его математике.

